SWETの仕様分析サポートチーム所属のtakasek(@takasek)です。
仕様分析サポートチームでは、社内のプロダクト開発に対する形式手法の活用可能性を模索しています。当ブログでも、継続的に形式手法に関する情報発信をしています(形式手法 カテゴリーの記事一覧)。
当記事は、Kuniwak(@orga_chem)により社内開催されたAlloyガイダンスを元に再構成した記事です。よく知られたデータ構造であるStackを形式仕様記述しビジュアライズすることで、Alloyの使い方と利点を実感できます。Alloy未経験者でもステップバイステップで試せるように構成しました。是非、お手元にAlloyをインストールして読み進めてください。環境はAlloy 5.1.0を想定しています。
https://github.com/AlloyTools/org.alloytools.alloy/releases
Alloyとは
形式手法の言語およびツールです。システムの構造の制約や振る舞いを簡易に、しかし強力に記述できるようデザインされています。記述されたモデルは要素同士の関係グラフとして視覚化できるというのが特徴です。
もっとも単純なモデルを記述する
Alloyのエディタを起動したら、以下を記述してください。
sig A {}

sig はsignatureを意味し、atom(要素)の集合を示します。signatureはオブジェクト指向プログラミングのclassと書き方がなんとなく似ていますが、その実態はまったく異なるものなのでご注意ください。
Executeの結果
ExecuteボタンをクリックするとVisualizerが開きます。Visualizerでは、Nextボタンをクリックするたびにインスタンスが次々とグラフとして表示されます。インスタンスというのは、関係における変数を特定の値で束縛したものです。1

Aのatomが0, 1, 2, 3, 4個存在する例を確認できました。現実的には当然5個以上になることもありますが、個数が増えると探索コストが急激に増大するためAlloyは割り切ってデフォルトの探索範囲を少なくしています。それでもおおよその反例は見つかるだろうという前提を小スコープ仮説といいます2。もし無限のケースについて正しさを証明したい場合は、CoqやIsabelleに代表される定理証明支援系の技術が必要になります。
2シグネチャの関係を記述する
sigを2つに増やして、その関係を記述してみましょう。
sig A {
b: B // 集合Aに属する各々のatomは、集合Bに属するただ1個のatomと関係を持つ
}
sig B {}
Executeの結果
抜粋すると…
| 関係 | グラフ |
|---|---|
| Aの要素:0個 Bの要素:1個 |
 |
| Aの要素:1個 Bの要素:2個 |
 |
| Aの要素:2個 Bの要素:2個 |
 |
| Aの要素:2個 Bの要素:2個 |
 |
最後の例があることは提示されて初めて気づく人も多いのではないでしょうか。このように、パターンを網羅的に目で見て確認できるのがAlloyの良いところです。
関係の多重度は、さまざまな形で表現可能です。
sig A {
b: B, // 1個の要素への関係
c: one C, // 1個の要素への関係(※省略はoneを意味する)
d: lone D, // 0〜1個の要素への関係
e: set E // 0個以上の要素への関係
// 他にもあります
}
Stackを表現する
ここからが本題です。Stackをモデルとして記述していきましょう。見慣れた連結リストです。
sig Stack {
value: univ,
next: lone Stack
}
Stack というsignature、すなわち集合を定義しました。
Stack は value と next という2つのフィールドを持つsignatureです。フィールド value は、Stackに属する各々のatomと、univに属するただ1個のatomとの関係を示します。フィールド next は、Stackに属する各々のatomと、Stackに属する0〜1個のatomとの関係を示します。なお、univは「あらゆるatomが属する集合」を意味しています。
(勘の良い方は、このモデリングに「おや?」と思われたかもしれません。後ほどその点にも触れますので、今はこのまま読み進めてください)
ここまで書けたら、Executeします。
ビジュアライズの結果を読み解く
結果を見る前に…
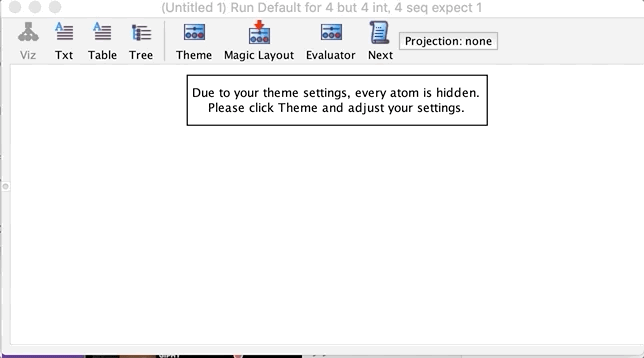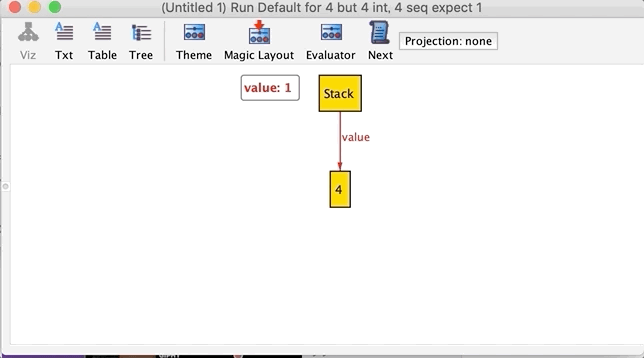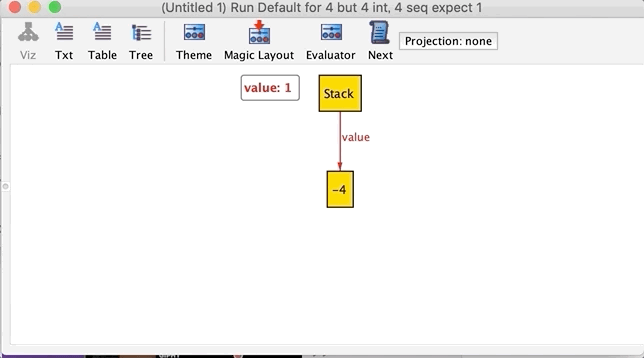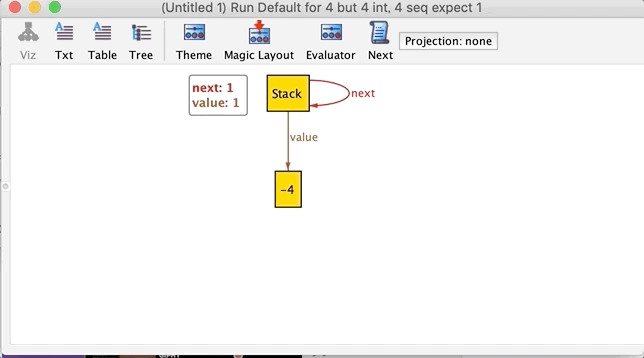
数値が変わるだけの同じような例が連続して出てきてキツいですね。よく見るとVisualizerのステータスバーに Run Default for 4 but 4 int, 4 seq expect 1 とあります。実はAlloyは、Executeの対象がない場合は暗黙的に以下のような出力命令が省略されているものと解釈しているようです(Alloy5現在)。
run{} for 4 but 4 int, 4 seq expect 1
for 以下は、Visualizerの表示要素数の範囲(スコープ)を示します。なお省略されたrunに任せず明示的に run {} と書いた場合には、 run{} for 4 but 4 int, 4 seq expect 1 よりも少量のインスタンスがビジュアライズされるようです。なぜそうなるのかは調査できていません。
ビジュアライズ結果を読み解く
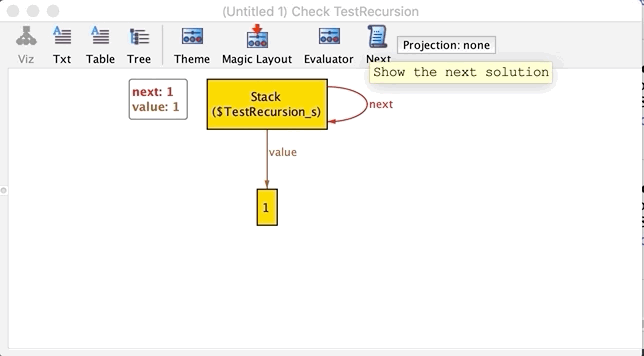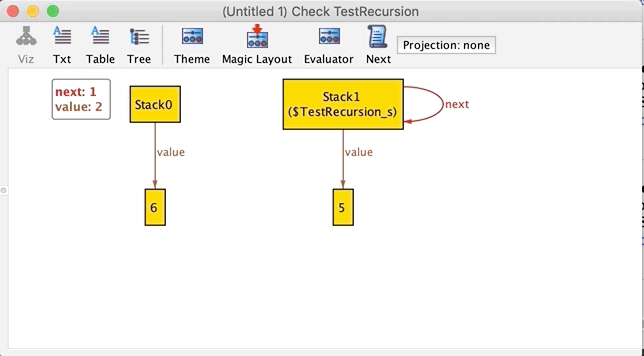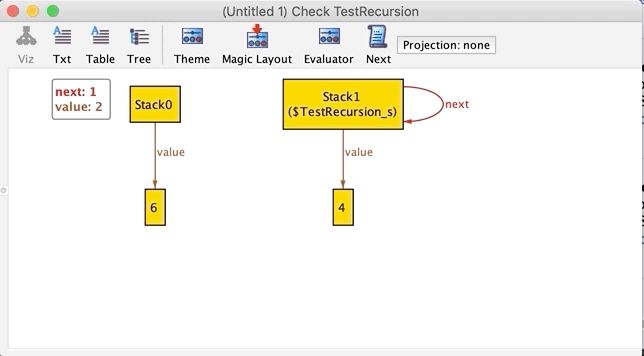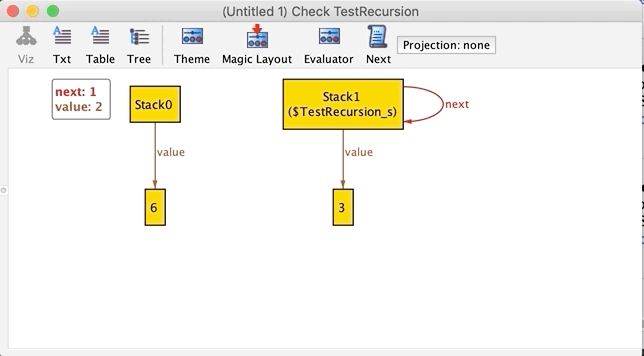
run {} で再度Executeして、ビジュアライズされた関係グラフを読み解きましょう。最初のグラフはこれですが…
いきなり想定外のグラフです。Visualizer上の Stack のnextが自分自身になっています。データ構造としてStackは循環を許しません。
「Stackは循環しない」という不変条件を書く
Stackが循環しないことを示すためには「このモデルは常にこうなる」という制約を与える論理式(不変条件)を書く必要があります。sig 内の記述だけに着目すれば成立するインスタンスでも、与えられた制約に違反する場合はビジュアライズされません。
「nextは自分自身にはならない」ことを示す
ただし不変条件を正しく書けなかった場合、正常なはずのインスタンスも表示されなくなってしまい、かつそれに気づけないリスクがあります。人間は異常なものを見つけることは得意ですが、あるべき正常なものの欠損に気づくのは苦手です。まずは論理式が本当に過不足のない制約を表現しているかを確認すべきです。
そのために表明(assert)を使います。不変条件はモデルに対して強制的に適用される論理式ですが、表明は現状のモデル自体には影響を与えず「モデルの制約はそうなっているはず」を表現する論理式です。3
今回、Stackが循環しないことを示すには「nextは自分自身にはならない」論理式を書きます。
// 「すべてのStackについて、自身のnextの集合に、自身が含まれない」という表明
assert TestRecursion {
all s: Stack | s not in s.next
}
// check命令は、表明に違反するインスタンスがないかを確認します
check TestRecursion
ツールバーから Execute > Check TestRecursion すると、コンソールに以下のようなメッセージが表示されました。
Executing "Check TestRecursion" Solver=sat4j Bitwidth=4 MaxSeq=4 SkolemDepth=1 Symmetry=20 483 vars. 72 primary vars. 827 clauses. 7ms. Counterexample found. Assertion is invalid. 3ms.
反例(counterexample)、すなわち現状のモデルの中で表明に違反するインスタンスが見つかりました。グラフとして確認できるので見てみましょう。
いいですね。「すべてのStackについて、自身のnextの集合に、自身が含まれない」の反例……すなわち「自分自身がnextになる」インスタンスだけが出力されています。表明をそのまま不変条件に昇格させれば「常にモデルがそれを満たす」という制約の記述になります。
記述全体は以下のようになります。不変条件の記述は fact です。
sig Stack {
value: univ,
next: lone Stack
}
fact NoRecursion {
all s: Stack | s not in s.next
}
不変条件を加えたモデルが想定どおりか、runして確認していきましょう。
run {}
すると、気になるものが見つかりました。
あるStack自身の循環はなくなりましたが、 Stack0.next が Stack1 、 Stack1.next が Stack0 という間接的な循環が残っています。
「nextを辿った先が自分自身にはならない」ことを示す
「nextは自分自身にはならない(s -(next)-> s)」ことは示しましたが、それだけでは足りなかったのです。 s -(next)-> ... -(next)-> s という関係を表現する必要があります。
そのためには推移閉包を使います。厳密な定義は置いといて、ざっくり言えば「関係Rについて s1 -(R)-> s2 s2 -(R)-> s3 が言えるとき s1 -(R)-> s3 も言える」という関係の集合が推移閉包です。Googleイメージ検索したら感覚は掴めると思います。Alloyには推移閉包オペレータがあり、 ^ をつけるだけで推移的関係を表現可能です。
……というのは本当でしょうか? 我々には確認の手段があります。Alloyの力を借りましょう。 fact NoRecursion はそのまま、表明を追加します。最初に書いたTestRecursionからの差分は、nextに推移閉包オペレータをつけただけです。
...
fact NoRecursion {
all s: Stack | s not in s.next
}
assert TestRecursion {
all s: Stack | s not in s.(^next)
}
// 似たようなIntの例が多すぎて邪魔なので、forでスコープを絞ってcheckします
check TestRecursion for 2 Int
再びツールバーから Execute > Check TestRecursion します。さっき見つけた双方向の矢印のパターンが反例として上がってくればしめしめです。どうでしょうか……
nextが双方向の矢印になる例だけが見つかりました。Stackの表示要素数が2個より多い場合の関係も検査してみましょう。
check TestRecursion for 2 Int, 4 Stack
3個のStackが循環参照している反例が見つかりました。いい感じです。
では、表明を不変条件に格上げします。
fact NoRecursion {
- all s: Stack | s not in s.next
+ all s: Stack | s not in s.(^next)
}
含意の確認をする
ちょっと待ってください。本当にこの格上げは正しいのでしょうか。推移閉包によって「nextを辿った先が自分自身にはならない」ことを表現できました。しかし、これを満たすとき、今までの「nextは自分自身にはならない」も満たすかと言われると確証がありません。感覚的には間違っていないように思えますが、論理の力で保証したいところです。
つまり、論理式「『nextを辿った先が自分自身にはならない』ならば『nextは自分自身にはならない』」が正しいことを確認したいのです。
assert TestImplies {
(all s: Stack | s not in s.(^next))
implies (all s: Stack | s not in s.next)
}
implies は含意、つまり論理学の初歩で習う「AならばB」です。
check TestImplies をExecuteすると、コンソールに以下のメッセージが表示されました。
Executing "Check TestImplies" Solver=sat4j Bitwidth=4 MaxSeq=4 SkolemDepth=1 Symmetry=20 560 vars. 72 primary vars. 907 clauses. 16ms. No counterexample found. Assertion may be valid. 2ms.
反例が見つからないということは、「『nextを辿った先が自分自身にはならない』ならば『nextは自分自身にはならない』」は正しいようです。不変条件の格上げは適切だと自信を持てました。
valueの不変条件を書く
ここまでで、全体の記述は以下のようになっています。
sig Stack {
value: univ,
next: lone Stack
}
fact NoRecursion {
all s: Stack | s not in s.(^next)
}
run {} for 1 Int
runの結果……
value周りにおかしな関係が見つかりました。「Stack0.next が Stack1」「Stack1.next が Stack1」など、あるStackのvalueがStackだったケースでは循環が生まれてしまうようです。
その原因は、valueの属する集合が univ すなわち「あらゆるatomの集合」になっているせいです。
どのように対処しましょうか。
- valueフィールドとnextフィールドの関係を適切に記述する
- 「valueはStackにならない」という仕様で逃げる
理想的なのは前者ですが割愛します。腕に自信のある方は正面突破してみましょう。今回は「valueはStackにならない」という仕様を導入して逃げることにします。より厳密な日本語で表現するなら「すべてのStackについて、自身と関係するvalueはStackではない」というべきでしょうか。
assert TestValue {
// ここに「すべてのStackについて、自身と関係するvalueはStackではない」という論理式を書く
}
もしあなたが手元にAlloyをインストールして進めているなら、ちょうどいい練習問題なので自分で書いてみましょうか。すこしスペースを空けますね。
...
...
...
...
...
答え合わせです。 答えのひとつは、次のとおりです。
assert TestValue {
all s1, s2: Stack | s1.value not in s2
}
check TestValue for 1 Int, 4 Stack で検査してみるといいでしょう。
論理式をリファクタする
実は all s1, s2: Stack | s1.value not in s2 はベストな解ではありません。よりシンプルに書くなら、
all s: Stack | s.value not in Stack
で十分です。
そういうことなら…と書き換える前に、一度立ち止まりましょう。プログラミングでもそうですが、リファクタリングでは修正前後に記述の意味が変化してしまってはいけません。論理の世界の言葉で言い換えると「修正前の論理式と修正後の論理式が同値である」ことを確かめたいです。
そこで、式変形前後での同値性の確認のテクニックを紹介します。手順は先述した含意の確認とよく似ています。
assert TestTrans {
(all s1, s2: Stack | s1.value not in s2)
iff (all s: Stack | s.value not in Stack)
}
iff は if and only if の略で「Bのときに限りAが成り立つ。Aが成り立つのはそのときに限る」つまり必要十分条件を示します。そのような論理式は同値として扱えます。オペレータとして <=> と書くこともできます。
check TestTrans をExecuteすると、コンソールに以下のメッセージが表示されました。
Executing "Check TestTrans" Solver=sat4j Bitwidth=4 MaxSeq=4 SkolemDepth=1 Symmetry=20 1158 vars. 69 primary vars. 2196 clauses. 7ms. No counterexample found. Assertion may be valid. 3ms.
反例が見つからないということは、修正前後の論理式は同値だということです。より大きなスコープで反例が見つかる可能性を頭の片隅に常に置いておく必要がありますが、今回は大丈夫でしょう。自信を持って書き換えましょう。なお、もし反例があった場合にはVisualizerでグラフとして確認可能です。Alloyは便利ですね。
完成したモデルを確認
sig Stack {
value: univ,
next: lone Stack
}
fact NoRecursion {
all s: Stack | s not in s.(^next)
}
fact NoRecursiveValue {
all s: Stack | s.value not in Stack
}
この記述が適切なものか確認しましょう。
run {} for 1 Int, 4 Stack
よさそうです。
push, popの前後関係をpredで表現する
データ構造のStackに対しては、pushとpopという操作が可能です。その確認もしたいです。
Alloyの状態モデルではミュータブルな手続きを書くことはできません。かわりに操作前後の状態を別物(事前状態、事後状態)として扱います。事後状態は慣習的に ' をつけて表記します。
- push前のStack =
s - push後のStack =
s'(読みはs-prime)
「s になんらかの値をpushした状態」と「s'」が同値だと示す論理式を書けば、前後の関係が表現できます。
任意個数の変数から真理値(true/false)を導く論理式を述語(predicate)といいます。これまで書いてきた run {} の {} も、実は述語です。このrun命令は、次のように分解できます。
pred P {} // 述語の宣言と定義
run P // 定義した述語に対する出力命令
pushを表現したいなら、次のような三変数述語になります。なお改行はandを示します。
pred Push[s, s': Stack, x: univ] {
s'.value = x
s'.next = s
}
この述語を満たす関係を run Push for 1 Int, 4 Stack でビジュアライズすれば、push前後のStackの関係が読み取れます。
上図の表記は、以下を意味します。
$Push_sはPushの変数のs$Push_s'はPushの変数のs'$Push_xはPushの変数のx
s に x をpushした結果が s' になることが図示できていますね。
popについても同じように書けます。難しいところはないので特に説明しません。練習問題として試してみるとよいでしょう。
まとめ
AlloyでStackを記述・検査する一連の流れを通じて、Alloyの使い方を紹介しました。とっつきやすいツールですので、是非ご活用ください。
仕様が妥当なものか確認せずに、手続き的に複雑な仕様を作り上げてしまうことはよくあります。形式仕様記述を用いて仕様をシンプルに書き、ときにリファクタしながら研ぎ澄ませると、より安全で自信に満ちあふれた開発プロセスが手に入るかもしれません。
なお、本記事よりも高度な記述が知りたい場合は公式のlanguage referenceをご参照ください。 https://alloytools.org/download/alloy-language-reference.pdf